MUNDO DE ARQUÍMEDES
Fracciones equivalentes
Fíjate en la siguiente imagen:
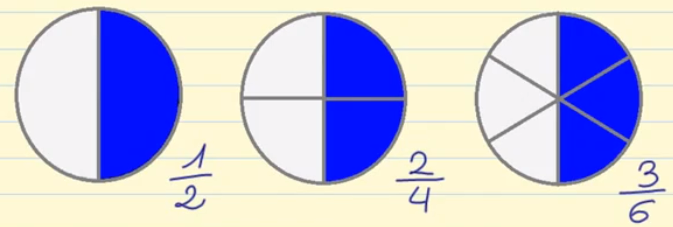
La primera figura está dividida en dos partes y hemos coloreado una de ellas. Por lo tanto, su fracción será 1/2.
La segunda figura la hemos dividido en 4 partes y hemos coloreado dos. Por lo tanto su fracción será 2/4.
Y la tercera figura la hemos dividido en 6 partes y hemos coloreado 3, por lo que su fracción será 3/6.
Si te fijas la parte coloreada en todas las figuras es la misma aunque las fracciones son diferentes: las tres fracciones dan el mismo resultado, son equivalentes.
RESPONDAMOS LAS SIGUIENTES INQUIETUDES¿Qué son las fracciones equivalentes?
Fracciones equivalentes son aquellas fracciones que representan la misma cantidad aunque el numerador y el denominador sean diferentes.
¿Cómo sabemos si dos fracciones son equivalentes?
Lo son si los productos del numerador de una y el denominador de la otra son iguales, es decir, productos cruzados.
Vamos a ver unos ejemplos:
Comprobemos si 2/5 y 4/10 son equivalentes.
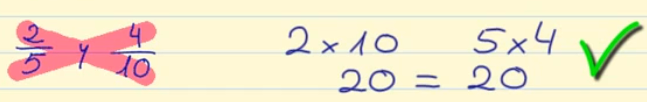
Para ello multiplicamos el numerados de una de las fracciones por el denominador de la otra.
2 x 10 = 20 5 x 4 = 20
Como el resultado es el mismo, podemos decir que 2/5 y 4/10 sí son fracciones equivalentes.
Ahora vamos a comprobar si 3/7 y 7/3 son fracciones equivalentes.
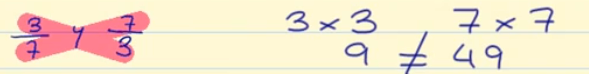
Para ello multiplicamos, como muestra la imagen:
3 x 3 = 9 7 x 7 = 49
Como el resultado no es el mismo, podemos decir que 3/7 y 7/3 no son equivalentes.
¿Cómo podemos calcular fracciones equivalentes?
Por amplificación
Multiplicando numerador y denominador por el mismo número.
Por ejemplo, partiendo de la fracción 1/3 y multiplicando el numerador y el denominador por el mismo número, podemos obtener diferentes fracciones equivalentes.
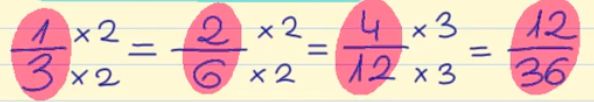
Si multiplicamos por 2: 1 x 2 = 2 3 x 2 = 6
por lo tanto la fracción 2/6 es equivalente a la fracción 1/3
Si volvemos a multiplicar por 2: 2 x 2 = 4 6 x 2 = 12
por lo tanto la fracción 4/12 es equivalente a 1/3 y a 2/6
Si ahora multiplicamos por 3: 4 x 3 = 12 12 x 3 = 36
por lo tanto 12/36 es una fracción equivalente a 1/3, a 2/6, y a 4/12
Por simplificación
Dividiendo numerador y denominador por un divisor común de ambos.

Por ejemplo, 12/30 podemos dividir el numerador y el denominador entre 2, ya que tanto el numerador como el denominador son pares.
12 : 2 = 6 30 : 2 = 15
por lo tanto 6/15 es una fracción equivalente a 12/30
Ahora podemos dividirlos entre 3.
6 : 3 = 2 15 : 3 = 5
por tanto las fracciones 2/5, 6/15 y 12/30 son equivalentes.
ACTIVIDAD ASINCRÓNICA
HAZ CLIC AQUÍ PARA DESCRAGAR LA ACTIVIDAD
Multiplicación y división con fracciones
Multiplicación de fracciones
Para multiplicar fracciones:
Se multiplican sus numeradores y sus denominadores:
Vamos a ver otros ejemplos:
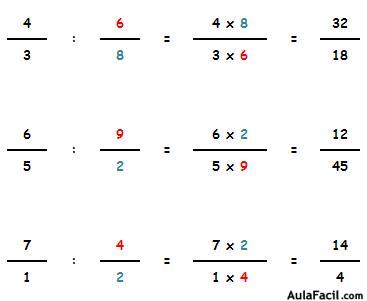
División de fracciones
Cuando se dividen 2 fracciones:
La fracción resultante tendrá:
Como numerador: el resultado de multiplicar el numerador de la primera por el denominador de la segunda.
Como denominador: el resultado de multiplicar el denominador de la primera por el numerador de la segunda.
Vamos a ver otros ejemplos:
Cuando dos o más fracciones tienen denominadores distintos se dicen heterogéneas. No es posible sumar este tipo de fracciones como se hizo con las homogéneas, debido a que representan distintos tipos de objetos. Observa el siguiente ejemplo, realicemos la suma .
Si representamos las unidades con círculos entonces las expresiones y se pueden representar así:
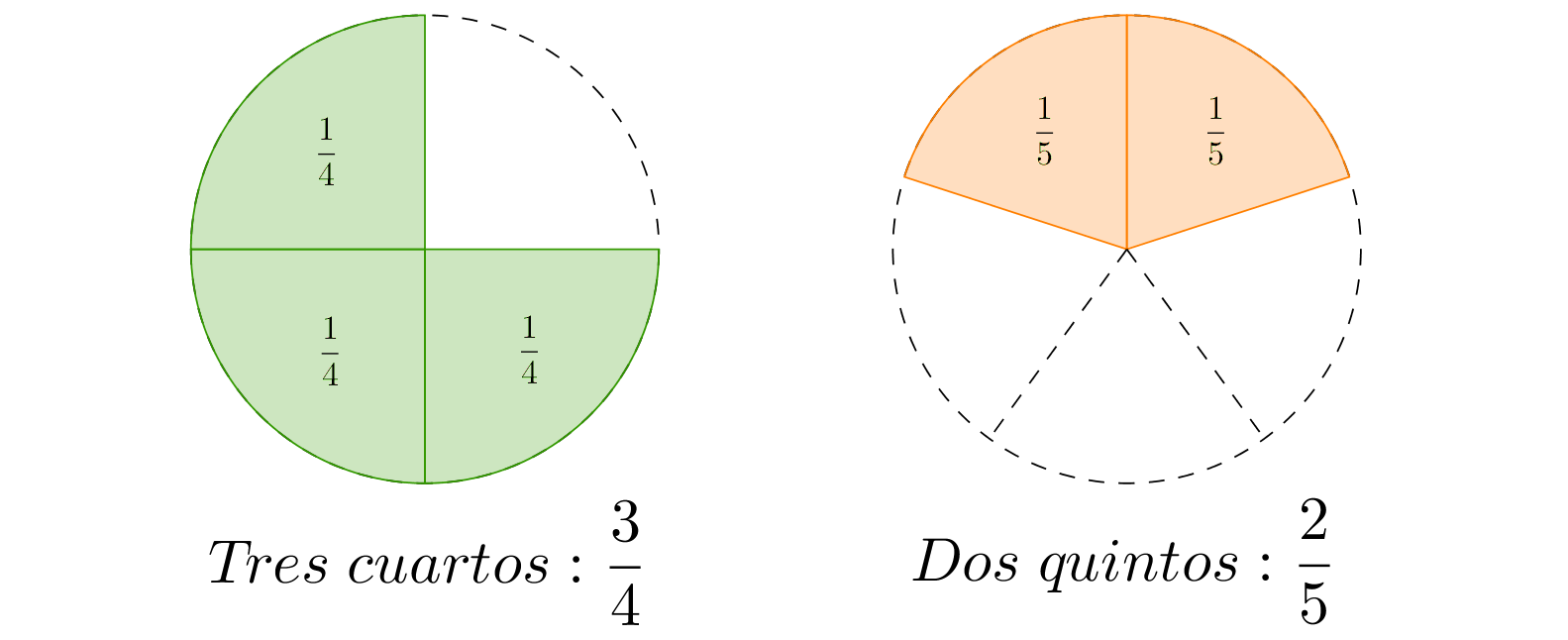
SUMA Y RESTA DE FRACCIONES HETEROGÉNEAS
Para realizar el procedimiento de una suma se usa la fórmula:
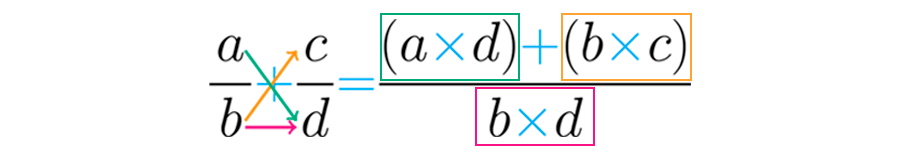
Ejemplo:
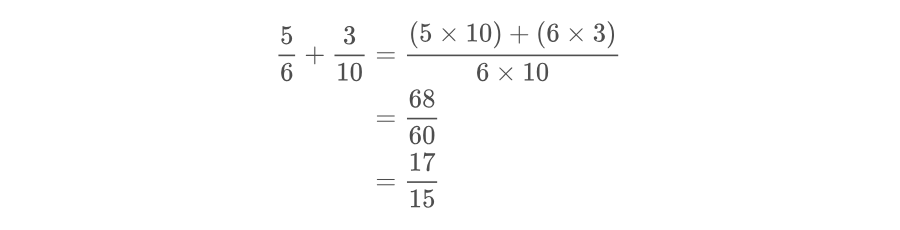
Podemos hacer un procedimiento de simplificación adicional al terminar el proceso.
En este caso el resultado de la suma es sesenta y ocho sesentavos, sin embargo después de simplificar se puede decir que es diecisiete quinceavos.
Es posible usar este mismo procedimiento para sumar más de dos fracciones.
RESTA
El procedimiento que se usa para restar es una fórmula similar a la de la suma, lo único que cambia es el signo:
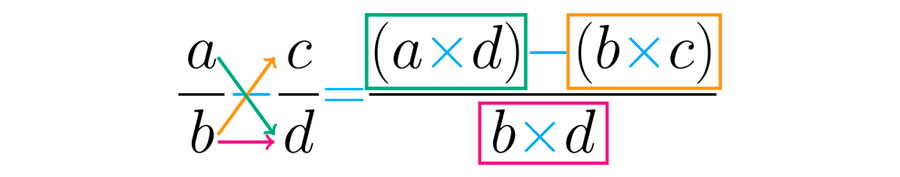
Esta semana vamos a introducir un concepto muy importante para realizar operaciones con fracciones: las fracciones homogéneas y las fracciones heterogéneas.
Para empezar, vamos a recordar los términos que componen toda fracción.
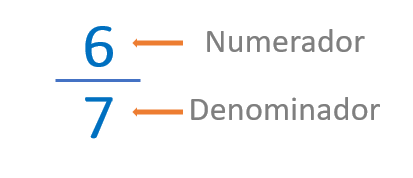
El termino que indica el número de partes en las que dividimos la unidad se llama DENOMINADOR.
El termino que indica el número de partes a las que nos referimos se llama NUMERADOR.
Una vez hemos recordado esto, vamos a ver la relevancia que tienen el denominador para comprender el concepto de fracciones homogéneas o heterogéneas.
Lo primero, es decir que se trata de un concepto que define un tipo de relación que existe entre dos o más fracciones y que depende del denominador que tienen dichas fracciones.
Dos fracciones son homogéneas cuando sus denominadores son iguales.
Que dos fracciones sean homogéneas significa que en ambas fracciones el denominador es el mismo, es decir, la unidad está dividida en la misma cantidad de partes y por ello sus denominadores son iguales.
Por ejemplo:
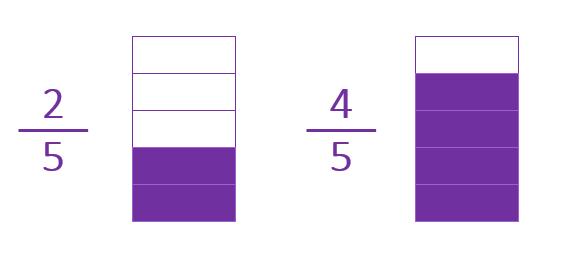
Estas dos fracciones son diferentes, pero su denominador es el mismo.
Por tanto 2/5 y 4/5 son fracciones homogéneas.
Dos fracciones son heterogéneas cuando sus denominadores son diferentes.
Que dos fracciones sean heterogéneas significa que en ambas fracciones la unidad está dividida en una cantidad diferentes de partes y, por eso, sus denominadores son distintos.
Por ejemplo:
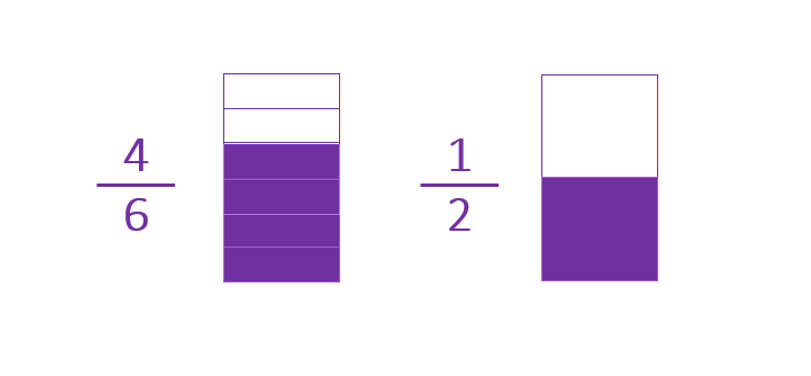
Estás dos fracciones son diferentes y sus denominadores también son diferentes.
Por tanto 4/6 y 1/2 son fracciones heterogéneas.
Ahora que tenemos claro estos conceptos podremos pasar al tema central de la adición de fracciones
Existen dos casos o modalidades posibles cuando nos encontramos sumando o restando fracciones:

FRACCIONES HOMOGÉNEAS
Para sumar o restar fracciones homogéneas, basta con operar los numeradores y conservar el mismo denominador.
Ejemplo:

En el ejercicio anterior podemos apreciar que se efectúo únicamente la suma entre los numeradores de las fracciones, y el resultado conserva el denominador de 4.
Resolviéndolo gráficamente tendríamos

Analicemos otro ejemplo pero ahora restando

En este ejercicio se efectúa la resta únicamente entre los numeradores y el resultado conserva el mismo denominador de 5.
Resolviéndolo gráficamente tendríamos

Después de leer y revisar la información anterior te invitamos a seguir aprendiendo con los siguientes videos.
LOGARITMACIÓN
RADICACIÓN / RAIZ CUADRADA
La radicación permite encontrar el número
que multiplicado por si mismo la cantidad
de veces que señala el índice
de la raíz, da como resultado un número dado.
Con la ayuda de los anteriores videos podrás tener una idea más clara de los temas propuestos en nuestro mundo.
Esta semana cerraremos el tema de la divisibilidad, para iniciar nuevos contenidos.
POTENCIACIÓN
POTENCIACIÓN DE NÚMEROS NATURALES: Una
multiplicación de varios factores iguales se puede expresar como una potencia.
Una potencia es una manera de escribir un producto de factores iguales.
Las potencias están formadas por una base
y un exponente.
Para leer una
potencia, se nombra el número de la base y el número del exponente, separados por la
expresión “elevado
a la”.
Ejemplo: 35 se lee: 3 elevado a la 5/ quinta
Potencia de 35 = 3 x 3 x 3 x 3 x 3 = 243
Teniendo en cuenta esta explicación realiza los siguientes ejercicios en casa.

Esta semana te invitamos a conocer las funciones y características de 2 de los reinos de la naturaleza
Esta semana te invitamos a conocer un poco más a cerca de los ecosistemas y su relación con los seres vivos
Para el reto de la sesión 3 en nuestro mundo te invitamos a conocer como funciona nuestro cuerpo y los sistemas que lo componen.
FICHA 1
2. Investiga acerca del "Hombre de Vitruvio" . Escribe las ideas en tu cuaderno para socializar en nuestro siguiente encuentro.
3. Realiza la siguiente lectura en compañía de tus familiares, socialicen sus ideas y escribe las dudas o preguntas que salieron de ellas para que sean socializadas la próxima semana.
'LA HISTORIA DE NADIA'
Nadia ya sabía que la vida no iba a ser fácil. Sus hermanas
eran esbeltas y graciosas y toda la familia siempre andaba resaltando sus
virtudes. Todo lo que hacían resultaba ser una maravilla ante los ojos de los
mayores. '¡Qué bien toca el piano Clotilde!'. '¡Qué dibujos más extraordinarios
pinta Margarita!', era lo que se oía en casa.
Sin embargo, Nadia era gordita y tímida, tanto, que si
la obligan a hablar acababa tartamudeando y entonces lo que se escuchaba era:
'Esta niña no sabe ni hablar'. Pero lo peor no era ser diferente, era que nunca
nadie le dijera que había hecho alguna cosa bien. '¿De verdad que no se hacer nada?', se preguntaba constantemente la
pequeña.
Al principio, siempre la regañaban por hacer mal las cosas.
'Te has equivocado', 'Eso no se hace así'. Pero poco a poco el tono fue
subiendo: '¡Fatal!', 'mira que eres manazas y rompes todo cuanto tocas'. Hasta
que llegó el día en el que escuchó la frase definitiva: 'No sabes hacer
nada, no vales para nada'. Desde entonces el silencio y las
lágrimas se impusieron en el corazón de Nadia.
Sin embargo, una noche, mientras lloraba sobre su almohada,
escuchó una vocecita lejana. Nadia enseguida reconoció en ella a su abuela y
después de mucho tiempo sonrió por primera vez. Desde entonces, todas las noches, Nadia
hablaba con el espíritu de su abuela, quien le repetía una y otra vez que algún
día descubriría su talento, su don. 'Si crees en ti podrás hacer bien todo cuanto te
propongas', era ahora la frase que repiqueteaba siempre en su cabeza.
Con el tiempo, Nadia se convirtió en una famosa
cocinera gracias a las que habían sido las recetas de su abuela. Pero lo
que realmente le hacía feliz era el momento de irse a la cama cada día y recordar todas las cosas
que había hecho bien ese día. Tras repasarlas, sonreía al espíritu de su abuela
y reconocía en voz alta que ella sí sabía hacer bien las cosas.
NOTA:
1. Realizar el siguiente ejercicio en línea para que practiques tus conocimientos al respecto. Para realizar el ejercicio HAGA CLIC AQUÍ.
Iniciamos nuestro segundo trimestre escolar
Esta semana te invitamos a conmemorar el día de la Tierra, ten en cuenta algunas de las recomendaciones dadas por el CAPITAN PLANETA en el siguiente video.
ACTIVIDADES SEGUNDA SEMANA 22-26/ 02/2021
Las actividades de esta semana se desarrollaron directamente en las sesiones y debiste enviar las evidencias al finalizar la sesión.
Si quieres recordar los temas vistos en el siguiente enlace encontrarás la presentación.
Recuerda que esta semana es de repaso y que trabajaremos con base a la guía entregada la semana pasada.
Haga clic aquí para ver la presentación de la clase de esta semana.
En nuestro mundo integraremos los conceptos y conocimientos de las asignaturas de Matemáticas y Ciencias Naturales , mientras aprendemos de manera divertida.








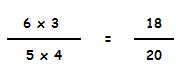
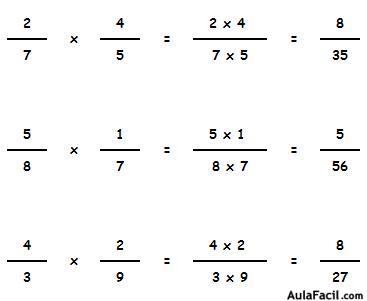
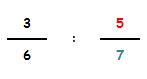
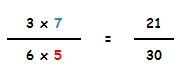





















































Comentarios
Publicar un comentario